Table of Contents
Introduction To Outlier Treatment
Outlier Treatment is One of the important part of data pre processing is the handling outlier. If your data contains outliers that affect our result which will depend on the data. So to remove these outliers from data Outlier Treatment is used. First of all, need to understand what is outlies.
What is Outliers?
“ Outliers is the value that lies outside the data”
Example: Long Jump A new coach has been working with the Long Jump team this month, and the athletes’ performance has changed.
● Augustus: +0.15m
● Tom: +0.11m
● June: +0.06m
● Carol: +0.06m
● Bob: + 0.12m
● Sam: -0.56m So here, Sam is an outlier
Following are two process to remove their outlies:-
- Interquartile Range ( IQR )
- Z-Score
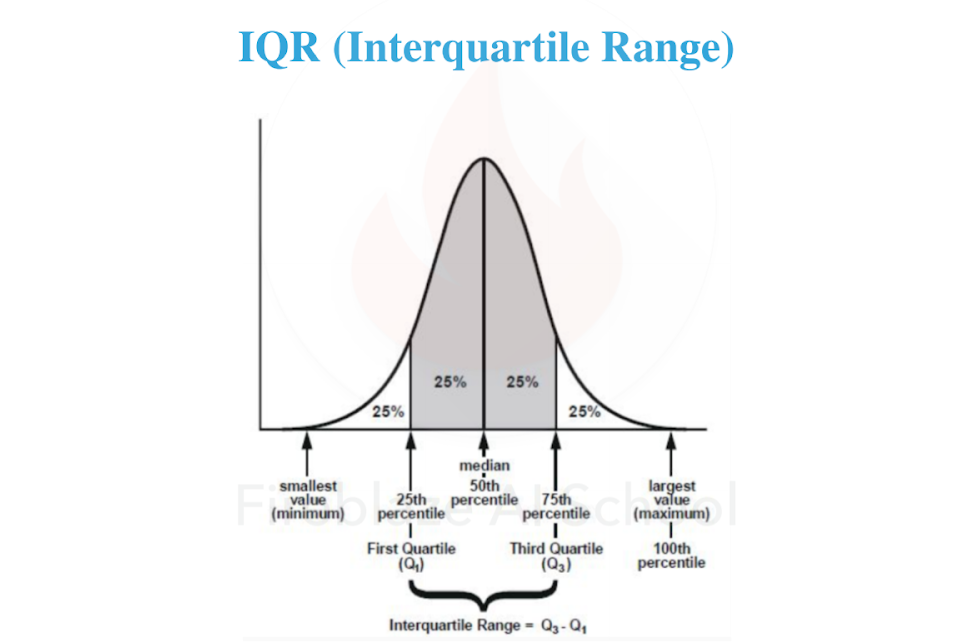
Interquartile Range( IQR )
Interquartile Range ( IQR ) equally divides the distribution into four equal parts called quartiles. It takes data into account the most of the value lies in that region, It used a box plot to detect the outliers in data.
The following parameter is used to identify the IQR range.
- 1st quartile (Q1) is 25%
- 3rd quartile (Q3) is 75%
- 2nd quartile (Q2) divides the distribution into two equal parts of 50%. So, basically it is the same as Median.
The interquartile range is the distance between the third and the first quartile, or, in other words, IQR equals Q3 minus Q1
Formula:- IQR = Q3- Q1
Steps to Calculate IQR
Step 1: Arrange data in ascending order from low to high.
Step 2: Find the median or in other words Q2.
Step 3: Then find Q1 by looking at the median of the left side of Q2.
Steps 4: Similarly find Q3 by looking at the median of the right of Q2.
Steps 5: Now subtract Q1 from Q3 to get IQR.
Widget not in any sidebars
Example:-
0, 12, 17, 4.5, 2.3, 17, 23, 14.6, 11, 10, 19.7, 20, 25, 2.3, 4.5, 10, 11, 12, 14.6, 17, 17, 19.7, 20, 23, 25
ascending order :- 0, 2.3, 2.3, 4.5, 4.5, 10, 10, 11, 11, 12, 12, 14.6, 14.6, 17, 17, 17, 17, 19.7, 19.7, 20, 20, 23, 23, 25, 25
14.6 is the Middle Value or Median or Q2
Consider: 0, 2.3, 4.5, 10, 11, 12 → 4.5 + 10 = 14.5/2 = 7.25 → Q1 Value
Consider: 17, 17, 19.7, 20, 23, 25 → 19.7 + 20 = 39.7/2 = 19.85 → Q3
IQR = Q3 – Q1 = 19.85 – 7.25 = 12.60 → IQR Value
Advantage of IQR
The main advantage of the IQR is that it is not affected by outliers because it doesn’t take into account observations below Q1 or above Q3.
It might still be useful to look for possible outliers in your study.
Widget not in any sidebars
Identify the Outliers Using IQR Method
As per a rule of thumb, observations can be qualified as outliers when they lie more than 1.5 IQR below the first quartile or 1.5 IQR above the third quartile. Outliers are values that “lie outside” the other values.
Outliers = Q1 – 1.5 * IQR OR
Outliers = Q3 + 1.5 * IQR

Outlier Treatment using IQR in Python
Example:- In this example, we load data set from the seaborn library and apply IQR outliers treatment on the total bill column.
Code:-
# Load Required Libraries
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
# Load DataSet From seaborn Library
data = sns.load_dataset('tips')
# To loda Data using sns.load_dataset('File Name')
data.head() # Check top five rows data
Output:-
total_bill tip sex smoker day time size
0 16.99 1.01 Female No Sun Dinner 2
1 10.34 1.66 Male No Sun Dinner 3
2 21.01 3.50 Male No Sun Dinner 3
3 23.68 3.31 Male No Sun Dinner 2
4 24.59 3.61 Female No Sun Dinner 4
# Apply IQR Method Into the Total bill Columns
# Detect Outliers Using Boxplot
# To detect outliers use box plot
sns.boxplot(data.total_bill)
plt.show()
# Scatter Point is Outliers
Output:-
# Apply IQR
# Calculate 1st quartile
Q1 = df1['total_bill'].quantile(0.25)
# Calculate 3rd quartile
Q3 = df1['total_bill'].quantile(0.75)
IQR = Q3 - Q1 # Formula Of IQR
print('Value of Interquartile Range :-',IQR)
Output:-
Value of Interquartile Range:- 10.779999999999998
# Calculate Lower Limit and Upper limit value to remove outliers
Lower_Limit = Q1 - 1.5 * IQR # Apply Formula To Calculate It
print('Lower Limit to detect outliers :- ',Lower_Limit)
Upper_Limit = Q3 + 1.5 * IQR # Apply Formula To Calculate It
print('Upper Limit to detect outliers :- ',Upper_Limit)
Output:-
Lower Limit to remove outliers:- -2.8224999999999945
Upper Limit to remove outliers:- 40.29749999999999
# Apply condition on total bill column to remove outliers from data
# 1st condition is if the value is less than the Lower Limit it consider as outliers
# 2nd condition is if the value is greater than the Upper Limit it consider as outliers
dfiqr = data[~((data['total_bill'] < Lower_Limit ) | (data['total_bill'] > Upper_Limit))]
# ~ is Used For removing the values which we take
# | (OR Logical Operator) EX:- T | T = T, T | F = T, F | T = T, F| F = F,where T = True,F = False
# In Above Code we used OR operator which takes all Outliers From total_bill column and (~) is used to remove this outlier.
# Check the Original Shape Of data and outliers Removal data shape.
print('Original data set shape :-',data.shape)
print('Removed outlier data set shape :- ',dfiqr.shape)
Output:-
Original data set shape:- (244, 7)
Removed outlier data set shape:- (235, 7)
Z – Score
Z-score is the number of standard deviations from the mean a data point is. It finding the distribution of data where mean is 0 and the standard deviation is 1 i.e. normal distribution data
Formula:- Z Score = (x – μ) / σ
x: Value of the element
μ: Population mean
σ: Standard Deviation A
“ z-score of zero tells you the values are exactly average while a score of +3 tells you that the value is much higher than average. ”
Bell Shape Distribution and Empirical Rule:-
If the distribution is bell shape then it is assumed that about 68% of the elements have a z-score between -1 and 1; about 95% have a z-score between -2 and 2, and about 99% have a z-score between -3 and 3.

So the Z-score of any value is less than -3 or greater than +3 the value is considered as outliers.
Outlier Treatment using Z-score in Python
Example:- In this example, we load data set from the seaborn library and apply Z-Score outliers treatment on the total bill column.
Code:-
# Load Required Libraries
import numpy as np
import pandas as pd
from pandas import Series, DataFrame
import matplotlib.pyplot as plt
import seaborn as sns
# Load DataSet From seaborn Library
data = sns.load_dataset('tips')
# To loda Data using sns.load_dataset('File Name')
data.head() # Check top five rows data
Output:-
total_bill tip sex smoker day time size
0 16.99 1.01 Female No Sun Dinner 2
1 10.34 1.66 Male No Sun Dinner 3
2 21.01 3.50 Male No Sun Dinner 3
3 23.68 3.31 Male No Sun Dinner 2
4 24.59 3.61 Female No Sun Dinner 4
# Apply IQR Method Into the Total bill Columns
# Detect Outliers Using Boxplot
# To detect outliers use box plot
sns.boxplot(data.total_bill)
plt.show()
# Scatter Point is Outliers
Output:-
# Apply Z-Score Outlier treatment process on total bill column
# import zscore function from scipy.stats library
from scipy.stats import zscore # To Apply Zscore Treatment
z = np.abs(zscore(data['total_bill'])) # Calculate the Z-score value of total bill
# The abs() function is used to return the absolute value of a number.
# Add Z Score column To Data Frame and add value in it
data['Zscore'] = z
len(data[data['Zscore']>3]) # Here we check how many number of outlier is detected by the ZScore
Output:-
4
# Remove Outliers From Total bill column using Z Score
# Get that data which zscore value is less than 3
data_z = data[data['Zscore']<3] # Store less then 3 Z-Score value To the Variable
print('Removed outlier data set shape :-',data_z.shape ) # Check The Shape Of data
Output:-
Removed outlier data set shape:- (240, 8)
Conclusion
In this blog, you get the clear understanding of the Outlier treatment processes like IQR & Z Score and its working and their implementation on the data set. It will really helpful to Remove outliers from data and it also improve your knowledge of data preprocessing concepts.










